Les plus grandes découvertes scientifiques ont été pour la plupart faites fortuitement, parfois même par des personnes qui ne sont pas des scientifiques chevronnés. Aujourd’hui, c’est autour d’un mathématicien amateur de résoudre un problème de math qui date de plusieurs décennies.
Une avancée de taille qui ouvre plus de perspectives, et permet d’avoir une nouvelle vision sur ce problème qui a longtemps fasciné les scientifiques et les chercheurs.
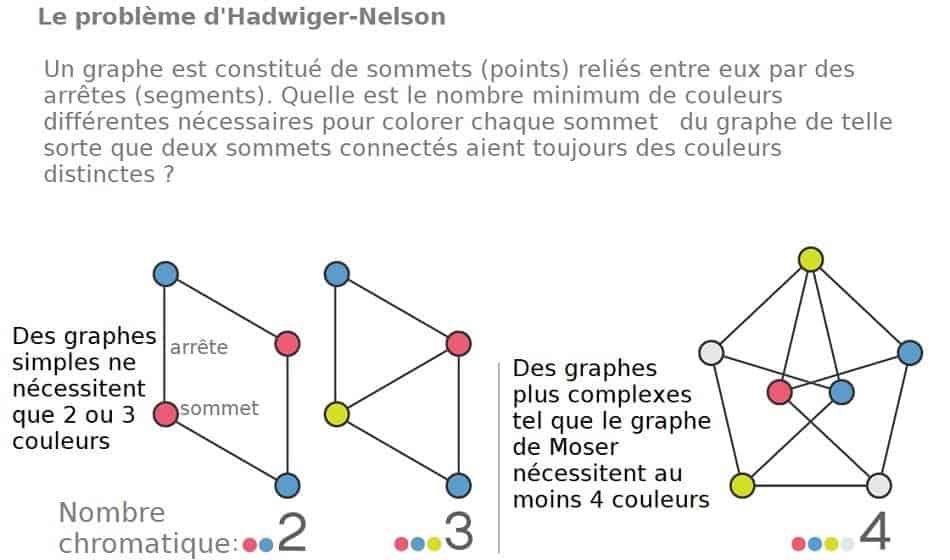
Le problème de Hadwiger-Nelson
C’est en 1950 que ce problème de math fut proposé par l’étudiant en mathématique Edward Nelson à l’Université de Chicago. Edward Nelson a mis au point un graphe composé d’un ensemble de points connectés par des arêtes à distance égale, l’ensemble repose sur un même plan.
La manœuvre consiste ensuite à colorier chaque point d’une couleur différente, en veillant à ne pas mettre la même couleur sur deux points qui ont la même relation. Le problème était de savoir combien de couleurs différentes sont nécessaires pour avoir des points connectés de couleur distincte.

Quelques années plus tard, Hugo Hadwiger, un mathématicien suisse, réussit à formuler et publier une variante du problème de Nelson. Il est alors baptisé « le problème Hadwiger-Nelson ».
De nombreux mathématiciens ont émis des théories autour du nombre chromatique, qui serait en fait compris entre 4 et 7. Mais jusqu’à présent personne n’avait réussi à donner une solution précise.
Un amateur pour résoudre ce problème
Dernièrement, Aubrey de Gray biologiste et ex-informaticien, a déposé un rapport de sa découverte sur arXiv intitulé « The Chromatic Number of the Plane is at least 5 » (le nombre chromatique du plan est au moins 5).
C’est en utilisant un fuseau Moser, composé de 7 points et de 11 arêtes, et en utilisant un logiciel informatique qu’il a pu fusionner un vaste réseau de 20 425 points connectés entre eux, pour ensuite diminuer le nombre à 1 581. Au fil des simulations, il a pu déduire qu’il fallait au moins 5 couleurs pour colorier les sommets du graphe sans avoir de répétition entre deux points connectés.
Mais c’est principalement grâce à sa passion et sa pratique compulsive du jeu Othello — un jeu particulièrement apprécié par les mathématiciens — qu’il s’est intéressé dans un premier temps au problème Hadwiger-Nelson.
De Gray a déclaré au Quantra Magazine qu’il a eu beaucoup de chance d’avoir pu faire avancer un problème vieux de plus de 60 ans, chose qu’on ne voit pas tous les jours. Le mathématicien Gil Kalai de l’Université hébraïque de Jérusalem, affirme que c’est vraiment intéressant d’avoir des avancées pareilles faites par des amateurs, ça permet de rajouter de la substance au domaine.
Depuis la publication de ces résultats, le mathématicien Marjin Heule de l’Université du Texas a réussi à construire un graphe à 5 couleurs avec seulement 826 sommets.
