Les mathématiques, qui sont un véritable cauchemar et un sujet épineux à ne surtout pas aborder — pour la plupart des étudiants — sont pourtant une partie de plaisir pour d’autres. Mais ce qui a toujours été un casse-tête pour des générations entières, ce sont bien les équations quadratiques.
Ce qui a été le plus pénible, pendant des millénaires, c’est d’apprendre cette formule et de la mettre en pratique, pour résoudre des problèmes du second degré. Alors qu’apparemment, cela n’était pas totalement nécessaire, d’après les déclarations d’un génie en maths, qui a une méthode nettement moins compliquée pour le faire.
Une astuce très ingénieuse
Il s’agit de Po-Shen Loh de l’Université Carnegie Mellon, qui a déploré le fait qu’un aussi grand nombre d’étudiants aient été contraints, aussi longtemps, de mémoriser un algorithme, datant de l’ancienne période babylonienne, sans que cela n’ait été entièrement indispensable.
Ce dernier servait à effectuer des calculs sur des équations sur aussi bien des équations quadratiques de forme typique, comme il est décrit ci-après ; ax 2 + bx +c = 0. Une ancienne étude de Loh, remontant à l’an dernier (septembre 2019), explique que cette méthode, peu commode, avait toujours été la seule capable de résoudre, avec précision et une fiabilité totale, des problèmes quadratiques.
Cela n’exclut toutefois qu’il y a eu d’autres possibilités, telles que la factorisation, la complétion du carré ou la cassure du papier millimétré. Il affirme, par contre, avoir découvert une alternative tout aussi efficace et beaucoup moins compliquée à utiliser. Tellement plus facile, qu’il s’étonnait de ne pas y avoir pensé auparavant !
C’est aussi simple que cela
Pour factoriser le quadratique x² + bx + c comme (x -) (x -), le mathématicien se base sur la somme pour calculer la moyenne au lieu du produit de deux nombres qui composent c.
Sur son site web, il explique que la somme de deux nombres est de 2 si leur moyenne est de 1. Il ajoute qu’il suffit de trouver un « u » de façon à ce que 1 + u et 1 – u soient les deux nombres et que u puisse avoir la valeur de 0.
Donc si l’estimation de u peut être fixée par cette nouvelle approche, aucune équation quadratique ne saura lui « résister ». Loh se dit très intrigué par le fait que ce procédé n’ait pas été découvert plutôt par les civilisations humaines qui se sont succédé au fil du temps.
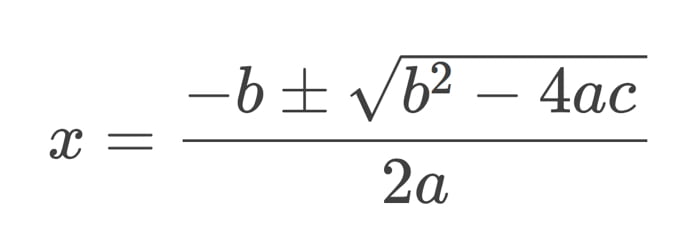
Wikipedia Commons
Cela est un mystère absolu, d’autant plus qu’on aurait été dispensé de mémoriser la formule quadratique, en adoptant la technique de Loh, dans tous les programmes officiels.
Bien entendu, d’autres articles de recherches similaires ont précédé celui de Loh. Le chercheur cite notamment, celui publié en 1989.
Quoi qu’il en soit, si tout se passe bien, celle-ci sera bientôt enseignée dans nos lycées et nos universités. Ainsi, l’algèbre sera, peut-être, un peu plus appréciée dans les milieux académiques. Avec un peu de chance, plus de gens y verront un domaine de recherche attrayant, et non un mystérieux labyrinthe sans issue.